
| 
|
EmergenceBiology 361 = Computer Science 361
| 
| 
|
Evolutionary Systems
Doug Blank27, 29 February 2006
|
|
|
|
I think we ought to be cautious in trying to characterize universal (or even modal) behavior of multiple ant systems. ... JoshCarp I modified Paul's last NetLogo program so that the ant doesn't base his moves purely on how successful a bold or safe move has been in the past, but rather on how successful each type of move has been from his current color patch ... PeterOMalley Is there an agent in a CA? ... BenKoski In agent based modeling ... the patches and turtles can operate under different rule sets. ... If we zoom out, then agents (living things) do appear to be operating under different rule sets than the spaces they occupy. ... AngadSingh By adding agents that follow different rules, we are cheating in the game of emergence. ... What is the difference between a glider in the Game of Life, and Langton's ant? ... DougBlank ...a challenge: is it so that there is a sequence of progressively sophisticated "emergent" models with progressively greater capabilities? ...PaulGrobstein There is a formula for calculating a digit of pi without calculating any of the previous digits of pi. ... I really believe that math is inherent in the universe AND that there is no frontier outside the reach of human intellect. Here's hoping. ... LauraKasakoff ...I noticed something very interesting: "emergence" is not considered a valid subject, at least in the eyes of the bibliographers who maintain the official Library of Congress subject headings.... BenKoski |
Evolutionary SystemsSearch, and Search SpacesYou can imagine that the parameters of a problem define a space of solutions. That is, every possible combination of parameters form a place in that space. Furthermore, imagine that each of those possible solutions has a quality (let's call it "goodness" or "fitness") that can be measured. This idea is called a fitness landscape. Such a landscape might look like these:
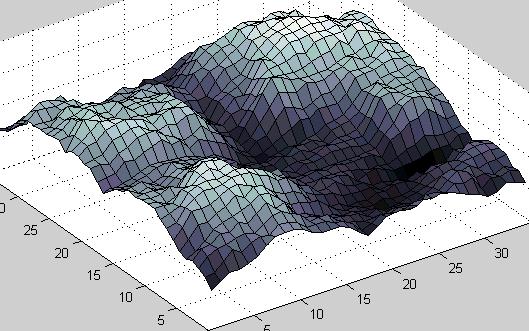
or, with just a single parameter, like this: 
The position on the x, and y axises represent the settings of two parameters, and the height represents the quality. If we knew what this space looked like, we could just go to the heighest peak. Unfortunately we don't know what the space looks like. So we have to resort to searching the space. Random Search
Hillclimbing
Simulated Annealing
Computational TemperatureSame as Simulated Annealing, but the temperature is not set by a schedule, but is calculated by how frustrated the hiker is. The temperature stays low until the hiker gets frustrated by being stuck, and then it climbs. The Genetic AlgorithmAs an analogy to biological evolution, the point in the landscape is the genotype, and the height of the fitness landscape is the fitness of the phenotype. Each parameter become a point in the simulated gene.
GA Demo: MastermindI'm thinking of a 56 letter phrase (26 letters + 1 space). How big is this space? 27 ^ 56 is 143341119796678074027577337316118932770382415738332565090012937927177499182473761. How long will it take you to search this space? Here is a Python program to search that space and find the phrase. It uses:
from pyrobot.brain.ga import *
phrase = "evolutionary systems are great methods to search a space"
size = len(phrase)
class PhraseGA(GA):
def fitnessFunction(self, i):
sum = 0
for c in range(len(self.pop.individuals[i].genotype)):
if self.pop.individuals[i].genotype[c] == phrase[c]:
sum += 1
return float(sum) / len(self.pop.individuals[i].genotype)
def isDone(self):
print "Best:",
self.pop.bestMember.display()
return (phrase == string.join(self.pop.bestMember.genotype, ""))
ga = PhraseGA(Population(300, Gene, size=size, mode='char',
verbose=1, elitePercent = .1,
crossoverPoints = 2),
mutationRate=0.06, crossoverRate=0.6, verbose=1,
maxGeneration=0)
ga.evolve()
Running the programOpen an editor (Applications -> Accessories -> Text Editor). Click the "Save" button, and name the file "evolve.py" and save it on your Desktop. Paste the above code into the file, and save it again. Open a terminal (Applications -> System Tools -> Terminal). Type in the terminal: cd Desktop python evolve.py Questions
Changing the Fitness FuntionCurrently, you only get a point for an exact letter match; you don't get any credit for being close. But we could change that! We could make it so that you get 1 point for an exact match, and as you get further away you get partial credit. You could first convert the letters into numbers, and then find their distance:
def myFitnessFunction(s1, s2):
alpha = "abcdefghijklmnopqrstuvwxyz "
fitness = 0
for i in range(len(s1)):
pos1 = alpha.find(s1[i])
pos2 = alpha.find(s2[i])
fitness += 1.0 - (abs(pos1 - pos2) / float(len(alpha)))
return fitness
Testing that gives:
>>> myFitnessFunction("a", "a")
1.0
>>> myFitnessFunction("a", "b")
0.96296296296296302
>>> myFitnessFunction("a", " ")
0.03703703703703709
>>> myFitnessFunction("abc", "abc")
3.0
>>> myFitnessFunction("abc", "abd")
2.9629629629629628
>>> myFitnessFunction("abc", "abf")
2.8888888888888888
>>> myFitnessFunction("abc", "aba")
2.925925925925926
>>> myFitnessFunction("abc", "abz")
2.1481481481481479
>>> myFitnessFunction("abc", "ab ")
2.1111111111111112
That seems like what we want. To use this as the fitness function:
from pyrobot.brain.ga import *
phrase = "evolutionary systems are great methods to search a space"
size = len(phrase)
def myFitnessFunction(s1, s2):
alpha = "abcdefghijklmnopqrstuvwxyz "
fitness = 0
for i in range(len(s1)):
pos1 = alpha.find(s1[i])
pos2 = alpha.find(s2[i])
fitness += 1.0 - (abs(pos1 - pos2) / float(len(alpha)))
return fitness
class PhraseGA(GA):
def fitnessFunction(self, i):
return myFitnessFunction(self.pop.individuals[i].genotype, phrase)
def isDone(self):
print "Best:",
self.pop.bestMember.display()
return (phrase == string.join(self.pop.bestMember.genotype, ""))
ga = PhraseGA(Population(300, Gene, size=size, mode='char',
verbose=1, elitePercent = .1,
crossoverPoints = 2),
mutationRate=0.06, crossoverRate=0.6, verbose=1,
maxGeneration=0)
ga.evolve()
Before running the code, what is your prediction? Will it evolve faster? How much faster? Ok, now run the code, and compare the results with your prediction. How did you fair? How do you explain any differences? Other experimentsConsider the 1D CA with radius 3 and 2 states (k). This is a very large space of possible rulesets (k ^ (k ^ (2r + 1))) which 340282366920938463463374607431768211456 different rulesets. Can you find a ruleset that does the density classification task? To evolve a ruleset, you simply need (k ^ (2r + 1)) or 128 zeros and ones. Every combination is a different ruleset. For more information see Revisiting The Edge of Chaos, and the local Python code /usr/lib/python2.4/site-packages/pyrobot/general/gaca.py. To run it, do: cd /usr/lib/python2.4/site-packages/pyrobot/general/ python gaca.py Limitations of GAsEvolving a phrase isn't much like real evolution (unless you believe in intelligent design. Why? What can we use GAs for? What else could we evolve? What couldn't we evolve? Genetic ProgrammingThe GA allows us to evolve a set of parameters. But it is still up to us to determine what each of those parameters means. How does that effect what we can evolve? There is another standard method for evolving solutions called genetic programming. In this model, genes are composed of programs parts. These programs are most often represented as what we call in computer science, "trees" or nested expressions. We use the language Lisp to represent these expressions. (By the way, NetLogo is also based on Lisp, but without the parentheses.) Consider evolving an experssion to compute something, like this: We can do something similar. In this example, there won't be any inputs, just the goal of evolving Pi:
from pyrobot.brain.gp import *
class PI_GP(GA):
def __init__(self, cnt, **args):
GA.__init__(self, Population(cnt, GPGene, bias = .6,
verbose = 1,
elitePercent = .1),
verbose = 1, maxGeneration = 25)
def fitnessFunction(self, pos, pr = 0):
diff = abs(self.pop.individuals[pos].eval() - pi)
if pr:
self.pop.individuals[pos].display()
print
return max(pi - diff, 0)
def isDone(self):
return abs(self.fitnessFunction(0, 1) - pi) < .001
share.env.update( {'+1': Operator(lambda obj: obj + 1, 1, "regular"),
'1/2': .5,
'e': math.e } )
gp = PI_GP(100)
gp.evolve()
In this example, we use:
After running this program for a bit, here is a typical example:
(+ (* (/ 1/2 (+ 1/2 e))
(+ (ifpos (+ 1/2 (+1 1/2))
(or (or (- e e) e) 1/2) 1/2)
(+1 (- (and (and e e) e) 1/2))))
e)
which is 3.1066878372. What, in general, do you notice about this solution? Try it yourself, with some variations. This is typical of evolved solutions. For example, let's watch a sample of Karl Sims evolved creatures: http://video.google.com/videoplay?docid=7219479512410540649Evolutionary algorithms have been said to be a perfect balance between exploration and exploitation. What does that mean? See Pyro Module Evolutionary Algorithms for more details on Python code examples. |