Serendip is an independent site partnering with faculty at multiple colleges and universities around the world. Happy exploring!
The Three Doors of Serendip: Generalizing
|
The Three Doors of Serendip:
Generalizing
|
Door images from Woodstone |
A good story to make sense of the Three Door problem is that probabilities can change. This is an especially useful explanation because it accounts for the fact that over time the more you switch rather than stay, the higher your winnings.
 At the outset, the chance that the prize is behind any given door is equal. It doesn't matter which door you choose. With three doors you have a 1/3 chance of picking door with the prize.
At the outset, the chance that the prize is behind any given door is equal. It doesn't matter which door you choose. With three doors you have a 1/3 chance of picking door with the prize.

However, once a door without the prize is opened, the probability of finding the prize behind the unopened door not selected increases to 2/3.
That probabilities describe likely outcomes, are not properties of objects (the doors) themselves, and that they can change with new information (opening doors) is also useful in that it can be generalized to other situations, i.e. games with more than three doors...
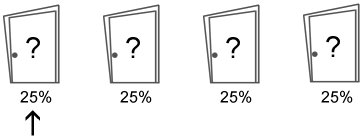
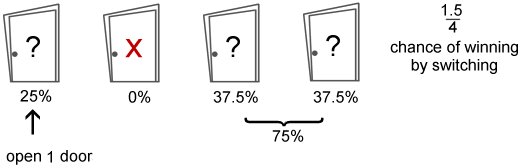
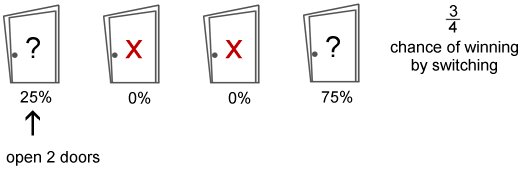
With four doors, at the outset the probabilities for each of the doors is equal (25% of hiding the prize). With new obersvations (opening one door, opening a second door) the probabilities assigned to the unselected and remaining unopened doors change. With four doors and one opened, you have a ~38% chance of finding the prize by switching to one of the two unopened doors. In this case, switching is only a slightly better strategy than staying compared to the three door version. However, when a second unwinning door is opened, your chance of winning by switching to the remaining door is 75%, then making switching an even better strategy in the long run compared to the three door version.
And so on...



|
Hands on understanding |
Experimental understanding |

Broader understanding |



Comments
Post new comment