Serendip is an independent site partnering with faculty at multiple colleges and universities around the world. Happy exploring!

The Three Doors of Serendip: Itemizing

The Three Doors of Serendip:

Itemizing

Door images from Woodstone

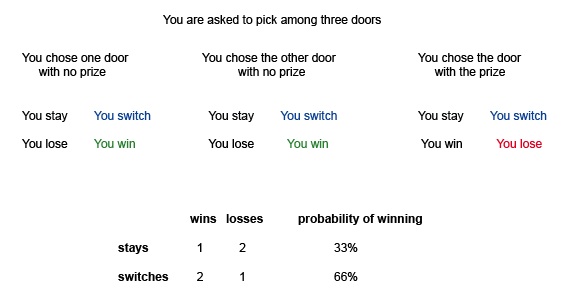
Itemizing, in cases where it's possible, may seem like the most "logical" way to reach a broader understanding. And sometimes it may. The table below shows a solution to the Three Door Problem reached by trying to list all possible cases and their outcomes. As you'll see, the itemization in this case yields the same conclusion that is observed empirically.

click to enlarge

Itemizing, though, does have problems of its own. It can be a very tedious process and one in which one can easily make mistakes. Second, there are a variety of different ways to itemize and different itemizations may yield different conclusions. The itemization below is different from the one above in that it defines cases differently and considers a greater number of them. And it yields a different conclusion. How is one to decide whether this itemization or the one above is better, if one doesn't have the empirical answer already?

click to enlarge

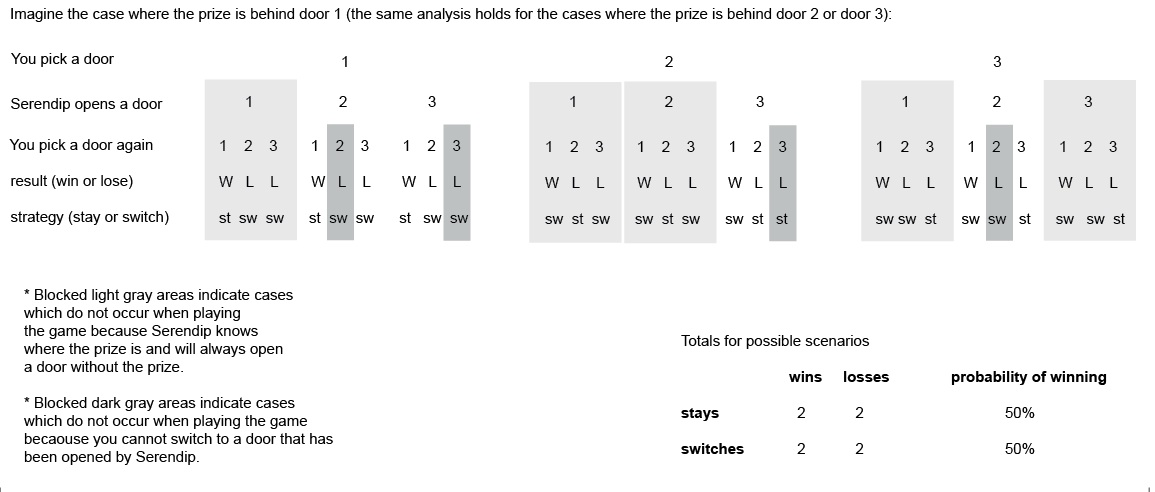
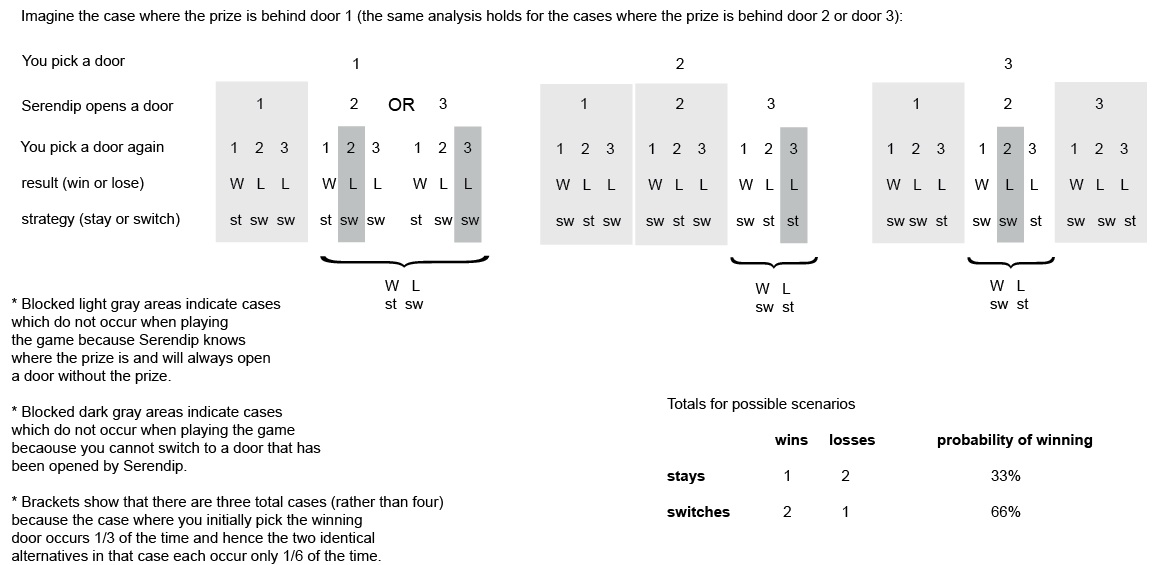
Below is an itemization like the one above, that does match the empirical conclusion because it has been modified to reflect the relative number of different times that different cases occur randomly. Would one know without the empirical observations that this modification is needed as a part of the itemization process?

click to enlarge

An additional problem with itemization is that it may or may not actually yield a sense of broader understanding (see The Four Color Problem). To put it differently, seeking broader understanding is seeking a sense of absence of conflict between various kinds of understanding and this may or may not result from itemization, even when it matches empirical observations.